Tavaly októberben értekeztem hosszabban az egyik legnépszerűbb Bitcoin körüli tévhitről: A kvantumszámítógépek fenyegetéséről. Most találtam egy igen látványos levezetést, ami kapcsán időszerűnek éreztem elővenni a másik igen népszerű témát: Nevezetesen, hogy vajon mekkora esélye van egy balanceszal rendelkező address privát kulcsának eltalálására? Közismert tény, hogy a privát kulcs->publikus kulcs->address transzformáció lépései között lényegében csak matematikai műveletsor van (ECDSA+2SHA256 és a végére még egy RIPEMD-160), tehát a megfelelő erőforrások bevetésével akár találomra el is lehet kezdeni végigpróbálgatni az összes lehetséges privát kulcsot mondván előbb-utóbb csak belefutunk egy olyan publikus kulcsba, ami mögött vagyon is található. Mivel a Bitcoin címek 256 biten képződnek, így a teljes címtartomány is 256 biten képződik. Jelenleg az UTXO táblázat 53.417.437 db tételt tartalmaz, tehát ennyi addressen van legalább egy morzsányi bitcoin.
A következő ábra azt mutatja be, hogy mekkora az eséllyel lehet beletrafálni egy értéket is tartalmazó privát kulcsba véletlenszerű próbálgatással, szemben mekkora esélye van a powerball nevű amerikai lottó megnyerésének. (5+1-et húznak 1-69-ig). A teljes powerball nyerési esélye egyébként lényegesen alacsonyabb a hazai ötös lottónál (utóbbiban kb 44 millió variáció nyerhet, az amerikai példában viszont 292 millió kombináció játszik).
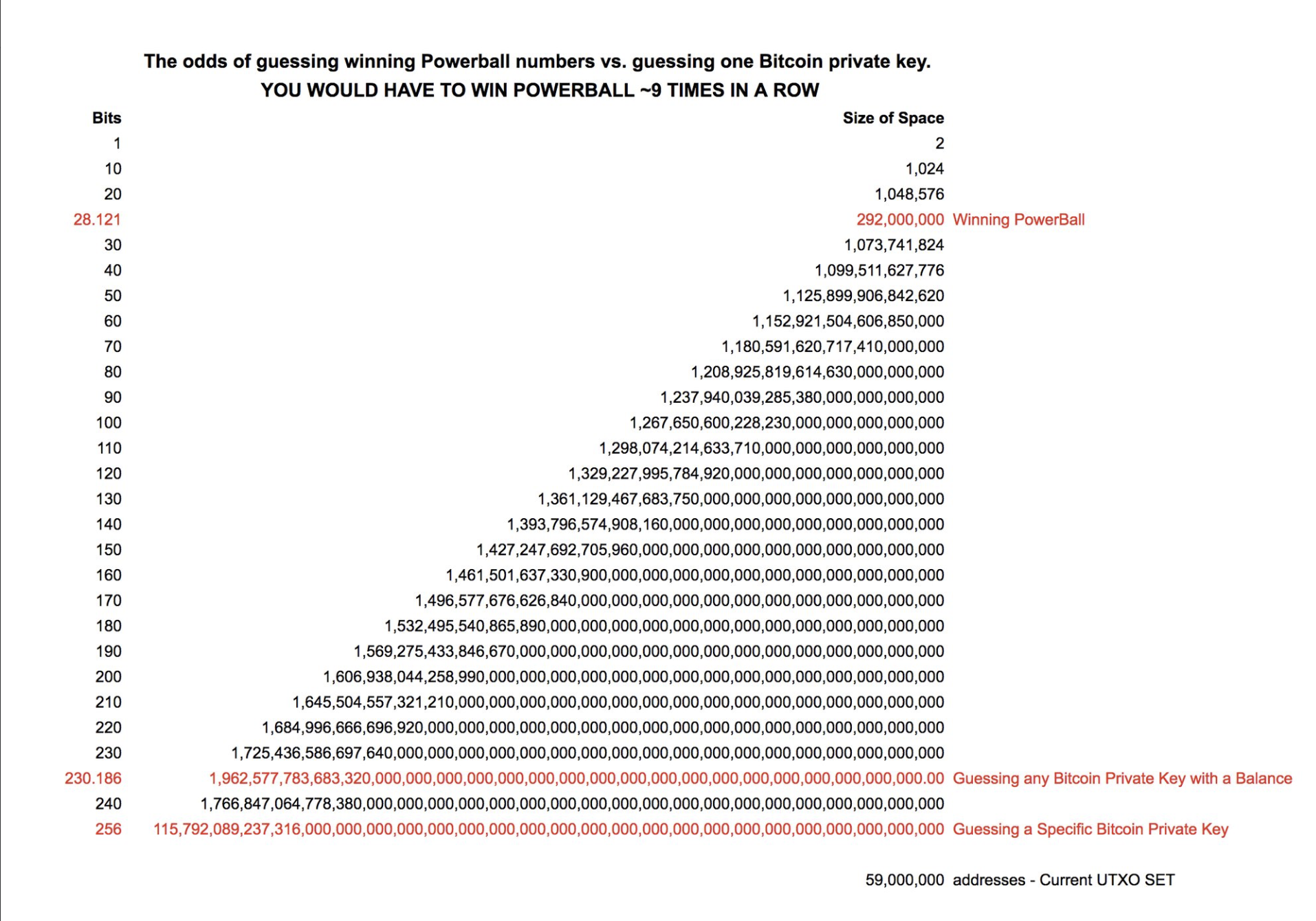
Az lista alapján akkora esélyed van beletrafálni egy balanceszal rendelkező address privát kulcsába, mint egyhuzamban megnyerni az ötös lottót egymást követő 11 alkalommal…
Persze az ilyen esetekben igen fontos az időtényező is. Hiszen lottót hetente sorsolnak, egy privát kulcsot viszont pillanatok alatt lehet generálni.
Mégis mennyi időt is vesz igénybe egy kulcsgenerálás? A jó hír az, hogy jelenleg nem nagyon létezik kulcsgeneráló ASIC és az ECDSA miatt nem is túlságosan valószínű, hogy valaha is létezhetne. Ellenben tele van a világ temérdek számítási kapacitással a GPU minerek miatt. Márpedig a privát kulcsból address generálásra a GPU tökéletes. Találtam némi statisztikát a vanity address generátorok kapcsán (apropó időszerű lenne lassan egy cikk a vanity addressekről is…). Ebből a következők olvashatók ki:
- 2 magos Corei5-2430M (2.4Ghz): ~660 KH/s
- 20 magos Xeon E5-2650L v3 (1.8Ghz): ~3MH/s
- 32 magos Xeon E5-2670 (2.6Ghz): ~6MH/s
- 1 GPU+Nvidia GRID K520 (4GPU): ~23MH/s
Tehát másodpercenként 23 millió kulcsot lehet egy ilyen géppel végig próbálni. Vegyük azt, hogy valaki rákölt erre a témára temérdek pénzt és felhalmoz 1 millió ilyen gépet. Ezzel a másodpercenkénti kapacitása már elérné a 23TH/s-t. Ez még mindig eléggé sovány performancia. Álmodjunk nagyot és feltételezzünk egy komoly generációváltást vagy akár egy keygenerator ASIC fejlesztést. Ezzel mondjuk talán el tudjuk érni a Bitcoin jelenlegi teljes network hashing powerét (23EH/s), amihez ugye kell egy Paksnyi atomerőmű áram is…
Na ha mindezzel megvagyunk, akkor immáron csak 2.705e+47 (270.577.970.750.242.640.000.000.000.000.000.000.000.000.000.000) évig kell üzemeltetni ezt az 1 millió ASIC-et, hogy biztosan találjunk legalább egy olyan addresst, amin létezik nullánál több bitcoin.





vanity address cikk várós, jöhetne tényleg 🙂
Ez mit jelent?
“privát kulcs->publikus kulcs->address transzformáció lépései ”
Nem elég csak a privát kulcsot eltalálni?
Vagy le kell ellenőrizni a publikus kulcsokat is a privát kulcs mögött?
Egy privát kulcsból nem tudod eldönteni, hogy azon van-e pénz. Ahhoz le kell képezni belőle előbb a publikus kulcsot, majd abból az address-t.
Több millió cím létezik már amin van bitcoin. Így nekünk nem a lottósorsoláshoz hasonlóan kell egyet megtalálni, hanem a sokmillió közül bármelyiket. Ez viszont sokkal nagyobb esélyt jelent, nem?
Akár osztható is a kapott eredmény (2.705^47 év) a címek számával.
Annak az esélyés mutatja az ábra és a számításom is, hogy beketrafálj akár csak 1 olyan címbe, amin van pénz is. Az ábra alsó sora mutatja annak az esélye, hogy egy konkrét cím privát kulcsát megtalálod.
A számot látva megnyugodtam. 🙂
Szia!
Egy észrevétel: 2.705^47 helyet 2.705*10^44 = 2.7058e+44 egyezik meg ezzel:
(270.577.970.750.242.640.000.000.000.000.000.000.000.000.000)
Amit írtál viszont: 2.705^47 = 2.051e+20= 2.051*10^20, azaz óriási a különbség (24 nagyságrend).
Egyébként ez is érdekes a cikk, így tovább!
próba: Sikerült az előző komment?
Igen, de spam karanténba került, gondolom a sok szám és pontot ip-nek nézte. Kiszedtem.
Egyébként köszi, javítom az OPot. Micsoda trehányság ez a részemről 🙂
Igen pici esély van, de ott az ici pici esély. Hiszen mekkora az esély, hogy egy emberbe 7x csapjon villám. Elenyésző, mégis megtörtént. https://en.wikipedia.org/wiki/Roy_Sullivan
És mekkora botrány lenne valaki egész véletlenül, és nem hatalmas számítási kapacitást bevetve megtalálna egy could waletet mondjuk az ethersecreten.
Annak az esélye, hogy valakibe 7x bele csapjon a villám igen kicsi, még akkor is, ha az egész életét vesszük alapul és figyelmen kívül hagyjuk, hogy az illető egy ranger, tehát egész nap a természetben bóklászik.
Ám ez az esély iszonyatos mennyiségű nagyságrendekkel NAGYOBB annál, minthogy én ma eldöntöm, hogy az életem hátralévő szakaszában egy alkalommal 7x egymást követően agyon fogom magam csapatni villámmal amiért tevőlegesen nem teszek semmi extrát, tehát nem kezdek innentől folyamatosan viharzónákban grasszálni.
Privát kulcsokat nem szoktunk nagy véletlenségből találni az utcán (villám analógia), hanem azért tevélegesen dolgozni kell.
Kis kiegeszites: a privkey valoban 256 bites, de az addressek csak 160 bitesek: minden cimnek van 2^96 db privat kulcsa, ami barmelyik elkoltheti az adott coint.
Persze meg igy is “nehany” milliard evig eltart egy kereses. 😀
Nekem myetherwalletten egyszer sikerült véletlenül belépnem egy másik tárcába, de üres volt és amúgy sem csináltam volna vele semmit, ha lett volna rajta bármilyen összeg is…Mondjuk az megrémisztett, hogy mennyire hasonló volt a private key, az enyémhez. Ma természetesen már nem írogatom be a private key-t, ez még régen történt, nem egy elütés különbség volt, hanem négyes-ötös blokkokban másoltam be a kulcsot és összekevertem a sorrendet. Először összefostam magam, hogy az egyenlegem 0 volt, aztán jöttem rá, hogy nem a saját tárcámban vagyok…
A privát kulcs egy kódolt formátuma a tényleges aes-128-ctr privát kulcs paramétereknek (iv, salt, mac, stb.). Mivel azon nincs semmilyen crc jellegű ellenőrzőkód, így teljesen normális, hogy 1-1 karakter elírásával is értelmes privát kulcs fog keletkezni, aminek az egyenlege nulla lesz, hiszen soha senki korábban nem használta még azt. A teljes kulcstér minden lehetséges variációjának nulla az egyenlege amit éppen nem használ senki.
Azaz, ha jól értem:
Egy karakter elírásával egy új privát kulcsot kapok, amit nagy eséllyel senki sem használt még.
Viszont használatban levő kulcs eltalálásához a cikkben említett esélyem van?
Ahogy mondod. Valójában a privát kulcs tér összes iterációja egy-egy privát kulcsot->publikus kulcsot->address-t rejt, amelyek brutálisan magas arányának az egyenlege nulla. A cikk erről szól.
Ez szinte lehetetlen!
Nincs meg véletlenül az a privát kulcsod?
Nagyon kíváncsi lennék rá!
Én akkor tudom elképzelni ha a private key ez volt:
0000000000000000000000000000000000000000000000000000000000000001
0000000000000000000000000000000000000000000000000000000000000010
Ezt ha négyes-ötös blokkokban másolod be és összekevered akkor tényleg 2 különböző számlára tudsz belépni.