Kissé nagy fába vágtam fejszémet a Machine Learning cikksorozatom kapcsán, amikor az előző fejezetben azt ígértem, hogy hamarosan konkrét alkalmazást fogok bemutatni a gépi tanuláshoz. Már persze nem az okozza fejtörőt, hogy élő példát mutassak az alkalmazásra, hanem, az hogy miként lehet ezt normálisan a blog keretei között bemutatni. Az ezzel kapcsolatos cikk vagy iszonyatosan hosszú lesz és szinte lehetetlen lesz követni, vagy pedig olyan tudásra kell hagyatkoznom, amivel az olvasó vagy rendelkezik, vagy nem. Ez utóbbi eléggé lutri. Ezért néhány kitekintő cikkel mutatom be a NumPy alapjait, ami egyébként lényegében az összes python alapú tudományos számítási és machine learning megoldás alapját is adja.
A numpy néhány alap funkcióját egy nagyon tipikus pénzügyi metóduson keresztül (Sharpe ratio számítás) mutatom be: Ennek lényege, hogy valamilyen ismert kockázatmentes portfolióhoz/termékhez képest kerül mérésre egy adott eszközalap vagy részvénypiaci termék teljesítményének szórását. Sharpe ratio lényegében egy referencia értéket ad meg, ami egységesen mutatja az adott eszközalap kockázat-hozam mutatóját.
Számítási módszere:
![]()
Ahol:
- rpt = Adott t időintervallumon belüli teljesítménye az eszközalapnak
- rrf = Egy tetszőleges kockázatmentes eszközalap hozama ugyanabban az időintervallumban
- t = időintervallum osztása (lehet napi, heti vagy akár havi is. Minél részletesebb annál pontosabb eredményt ad)
- n = interációs száma (mennyi különálló t időszak alatti hozamot veszünk figyelembe)
- op= Az „n” darabszámú „t” időszakra szóló eszközalap teljesítmények szórása.
A képlet egyébként jellemzően -1 és +3 közötti eredményt ad függően a vizsgált fundamentumoktól. Ennek értelmezése:
- mínusz érték: Jellemzően akkor jön ki, ha a vizsgált portfolió a vizsgált időszakban negatív eredményt ért el. Az ilyen esetekben a Sharpe ratio nem alkalmazható.
- 0 és 1 közötti érték: Azt mutatja, hogy a kockázatmentes eszközalaphoz képest a vizsgált eszközalap minden egységnyi kockázat vállalásra kevesebb mint egy egységnyi hozamot képes csak termelni.
- 1 és 2 közötti érték: Az előző pontból kiindulva itt fordul meg a kockázat/hozam arány. Tehát a vizsgált eszközalap esetén igaz, hogy a nagyobb kockázat kissé nagyobb hozammal jár.
- 2 és 3 közötti érték: Ide tartoznak a legjobb kockázat/hozam arányú eszközalapok, amelyekre igaz, hogy egységnyi kockázat legalább kétszer vagy többször magasabb hozammal kecsegtet.
Oké, ennyit az alapokról. Nézzük ennek a megvalósítását pythonban numpy segítségével. Kiindulási alapok:
- MySQL adatbázisban tárolt árfolyam adatok, melyek napi jegyzett záró árfolyamokat tartalmaznak termékenként. A sharpe kockázatmentes terméke legyen mondjuk tetszőleges HUF pénzpiaci alap. (Referenciának elmegy a KH HUF tőkevédett pénzpiaci alapja)
#!/usr/bin/python
import time, urllib, csv, re, time, sys
import MySQLdb as mdb;
import numpy as np;
try:
con = mdb.connect('localhost', 'user', 'pwd', 'schema')
cur = con.cursor()
except mdb.Error, e:
print "Error %d: %s" % (e.args[0], e.args[1])
sys.exit(1)
def column(matrix, i):
return [row[i] for row in matrix]
def find(l, elem):
for row, i in enumerate(l):
try:
if (i[0] == elem):
return row;
except ValueError:
continue
return -1;
Két releváns NumPy interpretáció a column() és a find() függvények. Előbbi visszaadja egy mátrixban tárolt adattömb egyik oszlopát arrayként, utóbbi pedig egy mátrix első oszlopában (esetünkben a dátum) keres egy fix értéket, ha megtalálja, akkor visszadja a mátrix sorát (arrayként), ha nem akkor a visszatérési érték: -1. Ezekre a függvényekre a mátrix normalizálásnál lesz szükség.
cur.execute("SELECT date,assetprice from assets where prodid="+xtag+" order by date desc limit 600");
x_matrix = cur.fetchall();
cur.execute("SELECT date,assetprice from assets where prodid="+ytag+" order by date desc limit 600");
y_matrix = cur.fetchall();
print len(x_matrix), len(y_matrix), len(x_matrix[0]), len (y_matrix[0]);
x_y_uniq = column(x_matrix,0) + list(set(column(y_matrix,0)) - set(column(x_matrix,0)));
x_y_uniq.sort();
x_last = x_matrix[len(x_matrix)-1][1];
y_last = y_matrix[len(y_matrix)-1][1];
X = [];
Y = [];
for row, i in enumerate(x_y_uniq):
X.append(float(x_last));
Y.append(float(y_last));
if (find(x_matrix, x_y_uniq[row]) != -1): x_last = x_matrix[find(x_matrix, x_y_uniq[row])][1];
if (find(y_matrix, x_y_uniq[row]) != -1): y_last = y_matrix[find(y_matrix, x_y_uniq[row])][1];
A fenti példa betölti a vizsált termék árfolyam adatait (xtag), majd a referencia kockázatmentes árfolyam adatait (ytag), ezek után elvégzi a két timeseries normalizálását. A normalizálásra azért van szükség, mert a Sharpe ratio minden vizsgált időpontban elvárja, hogy mindkét termék rendelkezzen arra az időpontra árfolyammal. Két különböző termék esetén azonban a két timeseries eltérhet, hiszen pl egy HUF-ban jegyzett amerikai tőzsdei teljesítményt lekövető befektetési alap nem közöl árakat pl a USA nemzeti ünnepekre, azonban ettől még ugyanazon napokon lehet árfolyama a pénzpiaci hazai alapoknak. A normalizálás során két olyan mátrix jön létre (X és Y) amelyekben pontosan ugyanazok a dátumok szerepelnek az árfolyamok pedig sorfolytonosak. Ahol nincs az adott napra jegyzett árfolyam, ott az utolsó napi érvényes árfolyam kerül újra alkalmazásra.
_SUMdiff = 0.0;
_Xstddev = [];
for row, i in enumerate (X):
if row%20 == 0:
_SUMdiff += ((X[row]/X[row-20]-1)*100) - ((Y[row]/Y[row-20]-1)*100);
_Xstddev.append((X[row]/X[row-20]-1)*100);
_recSUMdiff= float(float(1/float(row))*_SUMdiff);
A Sharpe számításhoz szükséges mátrix és tömb transzformációkra látható fentebb példa. A példa alapján látható, hogy a Sharpe-os 20 napos időeltolással számoltam. Ami nagyjából 1 hónapos időszakot fed le a munkanapokon közölt árfolyamadatok alapján. Az árfolyamok szórásnégyzetének számítása az előkészített _Xstddev tömb tartalma alapján már könnyedén számítható a NumPy segítségével: (np.std(_Xstddev)) és ebből már a Sharpe ration is könnyedén számolható: _recSUMdiff/np.std(_Xstddev)
[commercial_break]
print "uppersum",_SUMdiff;
print "1/n(uppersum) %d %.08f %.08f %.08f"%(row,_SUMdiff,(1/float(row)), _recSUMdiff);
print "stddev:",np.std(_Xstddev);
print "Portfolio return:",(X[row]/X[0]-1)*100;
print "Risk free portfolio return:",(Y[row]/Y[0]-1)*100;
print "Extra return over risk-free profit:",((X[row]/X[0]-1)*100)-((Y[row]/Y[0]-1)*100);
print "Sharpe (1/n) ratio:",_recSUMdiff/np.std(_Xstddev);
Releváns adatok kiíratása, úgy mind: vizsgált profolió és kockázatmentes portfolió elért eredménye, extra hozam a vizsgált portfolió javára és a konkrét sharpe ratio.
Egy minta futtatás ahol a KH Ázsia HUF alapjához kerül kiszámításra a Sharpe ratio. (referencia kockázat mentes portfolió: KH Pénzpiaci HUF alap):
[]$ ./sharpecheck.py –xtag 10 –ytag 597
stddev: 6.2789046435
Portfolio return: 25.7695501215
Risk free portfolio return: 5.13900589722
Extra return over risk-free profit: 20.6305442243
Sharpe (1/n) ratio: 0.00157330036675
Sharpe ratio: 1.03680494169
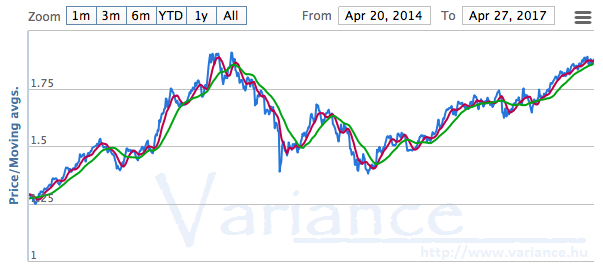
A vizsgálat egyébként 3 éves teljesítmény alapján történt. Az eredmény alapján látható, hogy a Sharpe Ration éppen csak, hogy meghaladta az 1.03-as értéket. Tehát a KH Ázsia alap esetén éppen csak, hogy igazolható, hogy az extra kockázat kis mértékben nagyobb profitot is eredményez. Elnézve az alap árfolyamát, ez a megállapítás gyanúsan megalapozottnak tűnik:
A KH alapkezelő portfoliójában (legnagyobb sajnálatomra) egyébként jellemzően elég kevés olyan alap van ahol a Sharpe ratio a saját kockázatmentes termékükhöz képest 2 közeli értéket tud felvenni. Egy konkrét ilyen példa a KH nagivátor alap:
[]$ ./sharpecheck.py –xtag 11 –ytag 597
Portfolio return: 81.9375742137
Risk free portfolio return: 5.13900589722
Extra return over risk-free profit: 76.7985683165
Sharpe (1/n) ratio: 0.00321821088844
Sharpe ratio: 1.95667222017
Anélkül, hogy nagyon titkot árulnék el: A Sharpe ratio módszere egy nagyon hatékony eszköze annak, hogy a látványos és hatalmas hozamokat ígérő “progresszív” termékek mögött rejlő kockázatokat is meg tudjuk érteni. A fenti minta implementáció segítségével bárki bővíteni tudja a meglévő pénzügyi eszköztárát ezzel az igen hatékony segédlettel. Nyilván a Share ratio önmagában pont annyira prediktív eszköz mint bármilyen más gépi tanulási módszer: A portfolió korábbi teljesítménye alapján von le következtetést a jövőbeli kockázatok kapcsán. Mindenki döntse el saját józan belátása szerint, hogy mennyire akar alapozni ilyen módszerekre.